A big issue in economics is the trade off between efficiency and equity.
- Efficiency is concerned with the optimal production and allocation of resources given existing factors of production.
- Equity is concerned with how resources are distributed throughout society.
- Vertical equity is concerned with the relative income and welfare of the whole population e.g. Relative poverty when people have less than 50% of average income. Vertical equity is concerned with how fairly resources are distributed and may imply higher tax rates for high income earners.
- Horizontal equity is treating everyone in same situation the same. e.g. everyone earning £15,000 should pay same tax rates.
For example, the Community Charge (Poll tax) was considered to be economically efficient because a poll tax doesn’t distort economic behavior. (e.g. doesn’t reduce incentives to work). However, by making a millionaire pay the same tax as a poor pensioner, it was considered to be unfair.
A tax on cigarettes can be said to increase social efficiency. The tax makes people pay the social cost of smoking. However, a cigarette tax is also highly regressive. It takes a bigger % of income from low income earners.
Pareto efficiency is concerned with creating a situation where we cannot make one party better off without making another party worse off.
For example, a country may devote 60% of GDP to the manufacture of armaments. In doing this, they may achieve technical and productive efficiency and produce on their production possibility frontier. Therefore from this perspective they are efficient. But, such an economy may have a great deal of inequality, with large portions of the population struggling to have enough to eat.
Bank Bailouts and Equity
From one perspective we may say bailing out banks is an economic necessity as it prevents a collapse in confidence in the banking system. By bailing out banks, we enable a more productively efficient economy. However, from another perspective it seems unfair that the government enables bankers to retain high paying jobs whilst they implement cuts for workers on lower income.Increased Inequality and Increased Growth
Sometimes, economic policies create a situation where everyone becomes better off (rising real incomes across population). However, those on high incomes gain a bigger % rise in real incomes. The result is that everyone becomes better off, but, there is also greater income inequality. Therefore, some people may feel that relatively they appear worse off compared to others in society.This is a pareto improvement in economic welfare but also an increase in inequality.
The final point is that there doesn’t have to be a trade off between equality and efficiency. An improvement in efficiency, should generally make the economy better off. There is no reason why improved efficiency has to lead to inequality. It is compatible to improve both efficiency and equity within society.

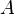 is preferred to a bundle
is preferred to a bundle 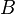 , and this bundle
, and this bundle  , then it is implied that the first bundle
, then it is implied that the first bundle  such that if bundle
such that if bundle 
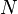 goods.
goods. and
and  , whose prices are
, whose prices are  and
and  , respectively. The consumer has a fixed amount of income,
, respectively. The consumer has a fixed amount of income,  , for spending on consumption, and his preferences are represented by a generic utility function,
, for spending on consumption, and his preferences are represented by a generic utility function,  , with
, with 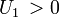 ,
,  .
The consumer’s aim is to obtain the maximum possible utility but he is
constrained by his level of income. He cannot spend more than
.
The consumer’s aim is to obtain the maximum possible utility but he is
constrained by his level of income. He cannot spend more than  1
1


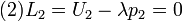

 and
and  imply that
imply that  .
That is, the marginal rate of substitution (MRS) must be equal to the
relation of prices, and it means that the indifference curve must be
tangent to the budget constraint.
.
That is, the marginal rate of substitution (MRS) must be equal to the
relation of prices, and it means that the indifference curve must be
tangent to the budget constraint.
 ,
, ,
, .They depend on prices and income, thus they can be written as
.They depend on prices and income, thus they can be written as  ,
, ,
, .The functions
.The functions  . Intuitively, it represents the maximum utility that the consumer can achieve for any given values of
. Intuitively, it represents the maximum utility that the consumer can achieve for any given values of  .
. .
It implies that the Lagrange multiplier can be thought as the marginal
utility of income. That is, it represents the rate of change of the
maximum utility that is derived from an infinitesimal rise in income.
.
It implies that the Lagrange multiplier can be thought as the marginal
utility of income. That is, it represents the rate of change of the
maximum utility that is derived from an infinitesimal rise in income. , but the monotonicity assumption ensures that he will spend all his income.
, but the monotonicity assumption ensures that he will spend all his income. .
Given this constraint, his objective is to reach this indifference
curve with the minimum possible expenditure. Therefore, the problem is:
.
Given this constraint, his objective is to reach this indifference
curve with the minimum possible expenditure. Therefore, the problem is: subject to
subject to 





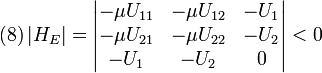
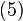 and
and 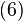 imply the same tangency condition than the UMP:
imply the same tangency condition than the UMP:  gives the optimal levels of
gives the optimal levels of 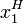 ,
, ,
, .The demand functions
.The demand functions  are the Hicksian (or Compensated) Demand Functions. Note that these demands depend on prices and the utility level, therefore they are denoted
are the Hicksian (or Compensated) Demand Functions. Note that these demands depend on prices and the utility level, therefore they are denoted  ,
, ,
, .
. . It is called the Indirect Expenditure Function and is denoted
. It is called the Indirect Expenditure Function and is denoted  .
. ,
meaning that the Lagrange multiplier represents the rate of change of
the expenditure function given a change in the utility level to reach.
,
meaning that the Lagrange multiplier represents the rate of change of
the expenditure function given a change in the utility level to reach.